A. Dinamika rotasi Benda Tegar
Dinamika rotasi adalah ilmu yang mempelajari tentang gerak rotasi (berputar) dengan memperhatikan aspek penyebabnya, yaitu momen gaya. Momen gaya atau yang lebih dikenal dengan torsi ini akan menyebabkan terjadinya percepatan sudut. Suatu benda dikatakan melakukan gerak rotasi (berputar) jika semua bagian benda bergerak mengelilingi poros atau sumbu putar. Sumbu putar benda terletak pada salah satu bagian dari benda tersebut.
Benda tegar merupakan benda yang tidak mengalami perubahan bentuk akibat pengaruh gaya, sehingga dalam melakukan pergerakan, benda tersebut tidak mengalami perubahan bentuk dan volume benda. Benda tegar dapat melakukan gerak translasi dan rotasi.
1. Momen Gaya/ Torsi (τ)
Apakah Momen Gaya/ Torsi Itu?
Untuk melihat suatu benda diam menjadi bergerak translasi
(lurus), anda perlu mengerjakan gaya
pada benda itu. Analog dengan itu, untuk membuat suatu benda tegar berotasi (berputar) terhadap suatu poros
tertentu, anda perlu mengerjakan
torsi (dari bahasa latin torquere; memutar) pada suatu benda. Momen gaya atau torsi (τ) merupakan besaran vektor yang mengakibatkan benda berotasi atau berputar. Besaran-besaran apakah yang berkaitan
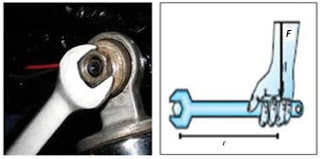
dengan torsi? Perhatikan gambar berikut !
Berdasarkan Gambar di atas, orang memberikan gaya kepada kunci sehingga kunci dapat memutar
baut. Baut berfungsi
sebagai sumbu rotasi, sedangkan perpanjangan
garis gaya disebut garis kerja gaya.
Jika gaya (F) yang diberikan tangan (garis
kerja gaya) tegak lurus terhadap
lengan kunci, maka lengan kunci ini
berfungsi sebagai lengan gaya.
Namun, jika gaya yang diberikan tidak tegak lurus
lengan kunci, maka lengan gaya merupakan
jarak yang tegak lurus dari sumbu rotasi dengan garis kerja gaya (r).
Untuk memahami komnsep
Momen Gaya /Torsi (τ), Perhatikan beberapa kejadian berikut
Sekarang Ananda coba perhatikan Gambar di atas, Untuk memutar baut, kedudukan tangan seperti gambar (c) lebih mudah dilakukan daripada kedudukan tangan pada gambar (b) dan (a). Sementara kedudukan tangan seperti gambar (b) lebih mudah dilakukan daripada seperti gambar (a). Gaya (F) yang diperlukan untuk memutar baut pada kedudukan (c) lebih kecil dari gaya yang diperlukan pada gambar (b) atau (a). Berdasarkan fakta ini, besar gaya putar atau momen gaya tidak hanya ditentukan oleh besar gaya, tetapi juga panjang lengan gaya (r). Hubungan ketiga faktor ini, diberikan dengan persamaan berikut
|
𝑟 = 𝒓 × 𝑭 atau |
Dimana :
τ = Momen Gaya (Nm)
F = Gaya
yang bekerja (N)
r = Lengan Momen (m)
θ = sudut yang terbentuk antara garis kerja gaya F terhadap lengan momen r
Seperti halnya gaya F, torsi τ juga termasuk besaran vektor, yang memiliki besar dan arah. Bedanya, arah torsi hanya dua, searah atau berlawanan arah jarum jam. Kedua arah torsi ini cukup dibedakan dengan memberikan tanda positif (berlawanan dengan perputaran arah jarum jam), atau negatif (searah dengan perputaran arah jarum jam.
Contoh Soal :
Tiga buah gaya bekerja pada batang AD yang bermassa 2 kg seperti pada gambar. Hitunglah resultan momen gaya terhadap titik B ! ( dimana g = 10 m/s²)
Jawab :
Untuk menentukan momen gaya yang bekerja pada titik B pada benda tegar AD yang bermassa 2 kg, maka uraian vektor – vektor gaya yang bekerja pada benda dapat diperoleh sebagai beriku
𝑟𝑩 = 𝑟𝑩𝑨 + 𝑟𝑩𝑬 + 𝑟𝑩𝑪
𝑟𝑩 = (−𝑟𝐵𝐴 . 𝐹1) + (−𝑟𝐵𝐸 . 𝑤) + (𝑟𝐵𝐶 . 𝐹3𝑦)
𝑟𝑩 = (−0,2 . 5) + (−0,25 . 2 . 10) + (0,55. 𝐹3 . 𝑠𝑖𝑛 300)
𝑟𝑩 = (−1) + (−5) + (1,1)
𝑟𝑩 = (−1) + (−5) + (1,1)
𝑟𝑩 = −𝟒, 𝟗 𝑵𝒎
Jadi, resultan momen gaya terhadap
titik B (B sebagai poros)
adalah 4,9 Nm
dengan arah searah putaran jarum jam
2. Momen Inersia (I)
Momen inersia (I) merupakan besaran yang menyatakan ukuran kecenderungan benda untuk tetap mempertahankan keadaannya (kelembaman). Pada gerak rotasi, momen inersia juga dapat menyatakan ukuran kemampuan benda untuk mempertahankan kecepatan sudut rotasinya. Benda yang sukar berputar atau benda yang sulit dihentikan saat berputar memiliki momen inersia yang besar, dan sebaliknya.
|
𝐼 = 𝑚. 𝑟2
Dimana :
I = Momen inersia (kgm2)
m = massa partikel (kg)
r = jarak partikel dari sumbu pusat rotasi (m)
Jika terdapat sejumlah partikel dengan massa masing-masing m1, m2, m3,... dan memiliki jarak r1, r2, r3, ... terhadap poros, maka momen inersia totalnya adalah penjumlahan momen inersia setiap partikel, yaitu sebagai berikut.
Atau secara pengintegralan dapat ditulis dengan persamaan:
𝑰 = ∫ 𝒓𝟐 𝒅𝒎
Berdasarkan konsep momen inersia I yang telah dipaparkan di atas, berikut beberapa persamaan momen inersia benda tegar yang teratur bentuknya dan berotasi pada sumbu tertentu seperti t e r t e r a pada gambar tabel berikut:
Menentukan Momen Inersia Benda Tegar dengan prinsip Teorema Sumbu Sejajar
Berdasarkan tabel di atas, kita telah mengetahui bahwa momen inersia batang silinder bermassa M dengan panjang L yang porosnya melalui pusat massa (tabel a) adalah 𝐼𝑝𝑚 = 1/2 𝑀𝐿2 Untuk mendapatkan Momen Inersia Batang silinder yang bergerak pada ujung batang maka dapat digunakan dengan prinsip Teorema Sumbu Sejajar dengan persamaan sebagai berikut :
𝐼𝑠 = 𝐼𝑝𝑚 + 𝑀𝑑2
Dimana :
Is = Momen Inersia titik pusat rotasi (Nm2)
Is = Momen Inersia titik pusat rotasi (Nm2)
Ipm = Momen Inersia benda di pusat massa (Nm2)
M = Massa benda (kg)
d = Jarak antara titik pusat massa ke titik rotasi (m)
sehingga untuk mendapatkan momen inersia batang silinder yang bergerak pada ujung batang dapat diperoleh :
𝐼𝐴 = 𝐼𝑝𝑚 + 𝑀𝑑2
𝐼𝐴 = 1/12
𝐼𝐴 = 1/12
𝐼𝐴 = 1/12
𝐼𝐴 = 4/12
𝐼𝐴 = 1/3
Berdasarkan uraian di atas dapat disimpulkan bahwa besar momen inersia benda tegar dipengaruhi oleh :
Bentuk atau ukuran benda,
Hubungan antara Momen Gaya (τ), Momen Inersia (I) dan Percepatan Sudut (α)
Untuk mendapatkan hubungan antara Momen Gaya (τ), Momen Inersia (I) dan Percepatan Sudut (α), maka kita dapat menganlogikan dengan menerapkan hukum Newton II translasi, yaitu : ∑𝐹 = 𝑚 . 𝑎 𝐹 = 𝑚 . 𝑎 𝐹 = 𝑚 . (𝑟. 𝛼) 𝐹. 𝑟 = 𝑚 . 𝑟 (𝑟. 𝛼) 𝐹. 𝑟 = 𝑚 . 𝑟 2 . 𝛼
Diperoleh 𝑟 = 𝐼 . 𝛼 atau
Dimana :
τ = Momen
Gaya (N.m)
I = Momen Inersia
(kg.m2)
α = Percepatan Sudut (rad/s2)
Contoh Soal :
Perhatikan gambar
berikut !
Sebuah silinder pejal berjari-jari 15 cm, dan bermassa 2 kg dijadikan katrol pada sebuah sumur seperti gambar di samping. Batang yang dijadikan poros memiliki permukaan licin sempurna. Seutas tali yang massanya dapat diabaikan, digulung pada silinder. Kemudian, sebuah ember bermassa 1 kg diikatkan pada ujung tali. Tentukan percepatan ember saat jatuh ke dalam sumur..!
Jawab :
Diketahui
Massa Katrol M = 2 kg
Jari-jari katrol r = 15 cm = 0,15 cm
Momen Inersia Katrol silinder pejal 𝐼 = 1/2 𝑀𝑅2
Massa Ember m = 1 kg
Ditanya
Percepatan Ember a = ...?
Dalam menjawab kasus seperti ini, Ananda harus mengidentifikasi benda- benda yang bergerak, dalam hal ini adalah katrol silinder pejal dan ember
Lihat Katrol (mengalami gerak rotasi)
perhatikan Gb. Ember pada soal (mengalami gerak Translasi)
Berlaku Hukum Newton II translasi
𝑚. 𝑔 − (𝐼) 𝑎 /𝑅2 = 𝑚. 𝑎
𝑚. 𝑔 = 𝑚. 𝑎 + (1) a/𝑅2
𝑚. 𝑔 = 𝑎 (𝑚 + 1/𝑅2)
a = m.g / (𝑚 + 1/𝑅2)
Dengan memasukkan nilai momen inersia I, maka dapat ditulis
𝑎 = 𝑚 . 𝑔 / (𝑚 + 1/2 𝑀𝑅2 /𝑅2)
𝑎 = 𝑚 . 𝑔 / (𝑚 + 1/2 . 𝑀)
𝑎 = 1 .10 / (1 + 1/2 . 2)
𝑎 = 10/2 = 𝟓 𝒎/s2
Jadi, percepatan yang dialami ember ketika menuruni sumur adalah 5 m/s2
Energi Kinetik Rotasi (Ekrot)
Benda yang berputar pada poros nya memiliki suatu bentuk energi yang disebut energi kinetik rotasi (Ekrot). Persamaan energi kinetik rotasi ini dapat diturunkan dari konsep energi kinetik translasi yaitu :
𝑬𝒌𝑻𝒓𝒂𝒏𝒔 = 𝟏/𝟐 𝒎 𝒗 𝟐
Dengan menganggap benda bergerak rotasi, maka kecepatan linier benda dapat ditulis
𝒓. 𝒗 = 𝒓. 𝜔 , sehingga diperoleh :
𝐸K𝑟𝑜𝑡 = 1/2 𝑚 (𝑟. 𝜔)2
𝐸K𝑟𝑜𝑡 = 1/2 𝑚 𝑟2 𝜔2
Sehingga persamaan Ekrot dapat ditulis :
𝑬𝒌𝒓𝒐𝒕 = 1/2 𝑰 𝑚𝟐
Dimana :
Ekrot = Energi
Kinetik Rotasi (Joule)
I = Momen Inersia benda
(kg.m2)
ῳ = Kecepatan Sudut benda (rad/s)
Contoh soal :
Sebuah silinder pejal bermassa 2 kg bergerak menggelinding dengan kecepatan 4 m/s. Tentukan besar Energi Kinetik yang dimiliki oleh silinder pejal tersebut.
(dimana momen inersia silinder pejal 𝐼 = 1/2 𝑀𝑅2)
Jawab :
Karena silinder pejal bergerak menggelinding, maka silinder pejal mengalami gerak transalasi dan rotasi, sehingga Energi Kinetik Total pada silinder pejal tersebut dapat ditulis :
𝐸𝑘𝑡𝑜𝑡 = 𝐸𝑘𝑡𝑟𝑎𝑛𝑠 + 𝐸𝑘𝑟𝑜𝑡
𝐸𝑘𝑡𝑜𝑡 = 1/2 𝑀 . 𝑣2 + 1/2 𝐼 . 𝜔2
𝐸𝑘𝑡𝑜𝑡 = 1/2 𝑀 . 𝑣2 + 1/2 (1/2 𝑀. R2) ( 𝑣/R)2
𝐸𝑘𝑡𝑜𝑡 = 1/2 𝑀 . 𝑣2 + 1/4 𝑀 . 𝑣2
𝐸𝑘𝑡𝑜𝑡 = 3/4 𝑀 . 𝑣2
𝐸𝑘𝑡𝑜𝑡 = 3/4 (2) . (4)2
𝑬𝒌𝒕𝒐𝒕 = 𝟐𝟒 𝑱𝒐𝒖𝒍𝒆
Jadi, besar energi kinetik silinder pejal yang menggelinding tersebut adalah 24 Joule.
3. Momentum Sudut (L)
Momentum sudut (L) didefinisikan sebagai perkalian silang antara vektor momentum linear benda p dan vektor posisi r.
𝑳 = 𝒓
× 𝒑
Secara matematis, penurunan persamaan momentum
sudut L dapat berawal dari konsep momentum
linier p, dan dapat ditulis:
𝒑 = 𝑚 . 𝒗
Dengan menganggap benda bergerak rotasi,
maka kecepatan linier
benda dapat ditulis
𝒗 = 𝒓. 𝑚
, sehingga diperoleh :
𝒑 = 𝑚 . (𝒓. 𝜔)
𝒑. 𝒓 = 𝑚. 𝒓. (𝒓. 𝜔)
𝑳 = 𝑚. 𝒓𝟐. 𝜔
Sehingga momentum sudut L persamaannya dapat ditulis : 𝑳 = 𝐼. 𝜔
Dimana :
L : Momentum sudut (kg. m2/s)
I : Momen inersia benda (kg.m2)
ῳ : Kecepatan sudut (rad/s
Hukum Kekekalan Momentum Sudut
Hukum kekekalan momentum linier menyatakan bahwa jika pada suatu sistem tidak ada resultan gaya yang bekerja (ΣF = 0) momentum linier sistem adalah kekal (konstan). Pada gerak rotasi jika tidak ada resultan momen gaya/torsi (Στ = 0) maka juga akan berlaku hukum kekekalan momentum sudut, sehingga secara konseptual dapat ditulis :
𝐿1 = 𝐿2
𝐼1. 𝜔1 = 𝐼2. 𝜔2
Hukum Kekekalan
Momentum Sudut berbunyi
:
“Jika tidak ada resultan momen gaya luar yang bkerja pada sitem (Στ = 0), maka momentum sudut didtem adalah kekal (konstan)”
Atau dapat ditulis : Jika 𝝉 = 𝒅𝑳 /𝒅𝒕 = 𝟎, maka 𝑳 = 𝒌𝒐𝒏𝒔𝒕𝒂n
Contoh soal :
Seorang penari balet yang berputar dengan lengan terentang dan kelajuan 3 rad/s memiliki momen inersia 12 kg.m². Jika saat lengannya merapat ke tubuh, momen inersianya menjadi 4 kg.m², maka berapakah laju putaran kecepatan sudut ketika lengannya merapat tersebut?
Jawab
Karena tidak ada gaya luar yang bekerja pada sistem penari balet tersebut,
maka berlaku Hukum Kekekalan Momentum
Sudut
𝐼1. 𝜔1 = 𝐼2. 𝜔2
(12 )(3) = (4) 𝜔2
36 = (4/36) 𝜔2
𝜔2 = 𝟗 𝒓𝒂𝒅/𝒔
Jadi, ketika tangan penari balet direntangkan, maka kecepatan sudut penari balet tersebut adalah 9 rad/s
B. Keseimbangan Benda tegar
1. Keseimbangan Statis Benda Tegar
Dari analisa uraian di atas, dapat disimpulkan bahwa secara matematis syarat suatu benda tegar mengalami keseimbangan statis adalah :
- Tidak ada resultan gaya yang bekerja pada benda tegar
∑𝑭 = 𝟎 dimana ∑𝑭𝒙 = 𝟎 dan ∑𝑭𝒚 = 0
- Tidak ada resultan momen gaya yang bekerja pada benda tegar
∑𝝉 = 0
Perhatikan Gambar di atas! Pemain akrobat berdiri di atas tali dengan membawa tongkat yang panjang. Pemain ini memegang tongkat tepat di tengah-tengah. Akibatnya, gaya berat tongkat pada setiap sisi sama besar. Gaya ini menimbulkan momen gaya pada sumbu putar (tubuh pemain akrobat) sama besar dengan arah berlawanan, sehingga terjadi keseimbangan rotasi. Ini menyebabkan pemain lebih mudah berjalan di atas tali.
Jenis – jenis Keseimbangan
Contoh Soal :
Perhatikan sistem keseimbangan berikut !
AC adalah batang homogen yang memiliki panjang 120 cm dan berat 22 N. Pada ujung batang, digantung sebuah balok dengan berat 40 N. Tentukan besar tegangan tali BC jika AB = 90 cm.
Jawab :
Perhatikan gambar uraian vektor dari kasus di atas !
AC = 120 cm = 1,2 m
wb = 22 N
w = 40 N
AB = 90 cm = 0,9 m
Ditanya: T = ... ?
Denga dalil Pythagoras, diperoleh
𝐵𝐶 = √902 + 1202 = 150 𝑐𝑚
Kemudian tinjau batang homogen sebagi benda yang mengalami gaya. Pada batang tersebut terdapat gaya berat balok, berat batang dan tegangan tali dalam arah sumbu Y
Bersaarkan syarat keseimbangan, dperoleh :
∑ 𝐹 = 0 dengan A sebagai orors
−𝑊( 𝐴𝐶 ) − 𝑊𝑏 (1/2 𝐴𝐶 ) + 𝑇 sin 𝜃 ( 𝐴𝐶 ) = 0
−40( 1,2 ) − 22( 0,6) + 𝑇 (90/150) ( 1,2 ) = 0
−48 − 13,2 + 0,72 𝑇 = 0
0,72 𝑇 = 61,2
𝑇 = 61,2/0,72 = 85 N
Jadi besar tegangan tali BC adalah 85 N
2. Titik Berat Benda
Titik berat benda adalah titik tangkap gaya berat suatu benda, di mana titik tersebut dipengaruhi oleh medan gravitasi. Penentuan letak titik berat ini dapat dilakukan dengan mudah apabila benda bersifat homogen dan beraturan (seperti kubus, bola, dan silinder). Titik pusat massa adalah titik yang mewakili posisi benda jika dianggap sebagai suatu titik materi.
Perhatikan gambar di bawah ini yang menggambarkan titik berat dari setiap partikel dalam suatu benda tegar.
- Benda berdimensi satu (berupa garis L)
- Benda berdimensi dua (berupa luasan bidang A)
Titik berat benda homogen berbentuk luasan bidang untuk beberapa benda dapat dilihat pada tabel berikut :
- Benda berdimensi tiga (berupa ruang volume V)
Titik berat benda homogen berbentuk ruang (volume) untuk beberapa benda dapat dilihat pada tabel berikut :
Contoh Soal :
Perhatikan gambar bidang berikut !
Jawab
Jadi koordinat titik berat pada bidang di atas adalah {0,2 : 3}
Demikian ulasan materi Semoga dapat bermanfaat.
Terima Kasih...!
.png)
0 Komentar
Terima kasih atas kunjungannya
Emoji